This is Part 3 of my nine-part series connecting financial frameworks with personal growth.

1.      Finance as a Framework

2.      Assets = Liabilities + Equity: What You Own Comes with Strings Attached

3.      Assets = Liabilities + Equity 2: What You Have vs. What You Can Use

4.      Time Value of Money 1: The Power of Compound Interest

5.      Time Value of Money 2: Why Humans Use Bad Discount Rates

6.      Risk and Return 1: No Risk, No Return

7.      Risk and Return 2: Why Humans Are Bad at Calculated Risks

8.      Risk and Return 3: Diversification and Building Multiple Pillars of Resilience

9.      Conclusion: The Emotional Balance Sheet

This week, we are discussing the most important concept in finance: compounding and the time value of money.

My post is going to be more mathematical than usual, not only because compounding is a mathematical concept, but also because I want to use math to illustrate how exponential growth applies to other areas of our lives. If you feel a desire to check out right now because you were told there would be no math, take a moment to slow down and notice that feeling. What do you feel resistant to?

Compound Interest

Two of my favorite quotes about time value of money from Al and Ben:

“Compound interest is the eighth wonder of the world. He who understands it, earns it; he who doesn't, pays it.” -Al

“Money makes money. And the money that money makes, makes money.” -Ben

Here is the classic time value of money formula:

Future value = present value * (1+growth rate)^time

Also written as

FV = PV * (1+r)^t

T is usually given in years, r is an interest rate and FV and PV are dollar amounts. For example, investing $1,000 for 20 years at a 7% interest rate will give you:

$1000 * (1.07)^20 = $3,869.68

*If this concept isn’t intuitive to you (it isn’t to most people), play around with my time value of money worksheet. It’s an Excel file that shows what an investment account will be worth given a fixed amount of investment each year, compounded over 40 years.

The example illustrates that even a small or moderate percentage return, left to compound over a sufficiently long period of time, can lead to a large increase on the initial capital investment. This is why the conventional wisdom about investing is “slow and steady wins the race.”

While people may understand compound interest conceptually, we often underestimate its long-term impact in other areas like skills or networking.

Do Things Other Than Money Compound?

Learning and skills certainly do.

Different mathematical models—linear, quadratic, exponential, logistic—apply to different phases of learning. The core point is that in most cases, learning offers better-than-linear returns on time spent. We’ll discuss each in turn.

Linear Growth

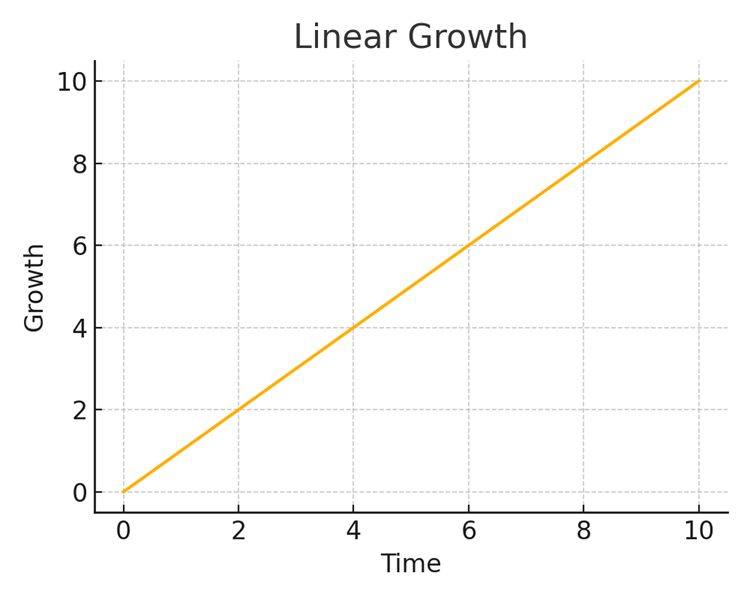
Learning grows linearly when we are memorizing discrete facts, like when we drill vocabulary for a new language. For every hour I study, I learn 10 new words or whatever the case may be.

Most learning has better-than-linear returns on time invested, because brute-force memorization is typically a small part of what most of us learn. Other than mastering basic vocabulary, numeracy, and some definitions and historical facts, we don’t typically need to memorize a lot of stuff.

Incidentally, since primary school education tends to be more memorization-based than college, it’s not surprising that a lot of people get turned off on education because they never get to experience anything better than linear growth.

Quadratic Growth

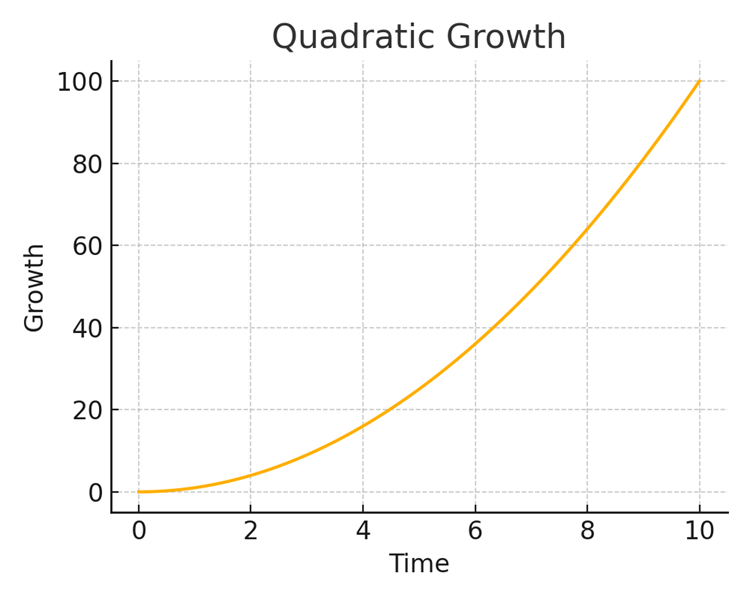
In the context of learning, quadratic growth applies when the mind starts to form connections between concepts. Understanding a new concept in any field doesn’t mean that the concept stands alone—your mind has the potential to draw a connection with every other concept you already know. The number of possible connections between concepts grows quadratically as you learn new concepts.

The relevant formula, also known as the “combination formula,” is:

N(N-1)/2

This formula describes how the number of connections (neural pathways) among nodes (neurons) in a network expands as the number of nodes expands. The “N-1” term means that a standalone node can’t have a connection to itself, and the “/2” part means that a connection from A to B is the same thing as a connection from B to A. We can see that as we add nodes to the network, the total number of connections among nodes grows much faster than the number of nodes grows.

Now, not every concept is likely to connect to every other concept. But to use a finance example, if I already understand concepts called “government bonds,” “municipal bonds,” and “corporate bonds,” learning a new concept called “private credit” doesn’t just mean that I know private credit, but I add three new connections between concepts. Adding a fifth concept called “repo markets” would mean I now get an additional four connections, and so on.

Exponential Growth

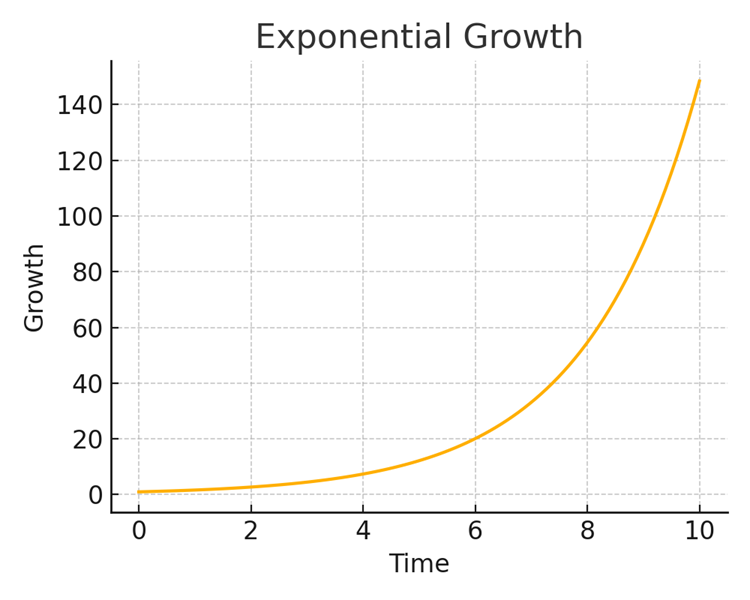
With exponential growth, growth accelerates faster and faster as the amount of time invested goes up. The curve slopes upward sharply because “time,” the variable, is the exponent in the formula:

FV = PV*(1+r)^t

In my view, there are significant exponential components to learning.

As we master foundational skills and concepts, additional knowledge on that topic becomes easier and easier to assimilate as our brain already has a well-established framework for the topic. For example, a person who was a multi-sport athlete in their teens and twenties will find it much easier to learn a fifth sport in their thirties or forties, as many of the basic movements needed for the new sport were already mastered learning the initial sports. The only thing the 40-year old needs to do is learn a few new movements and combinations of movements, the basic ruleset and objectives of the new sport, and integrate them into a large library of movements already mastered.

Logistic Growth

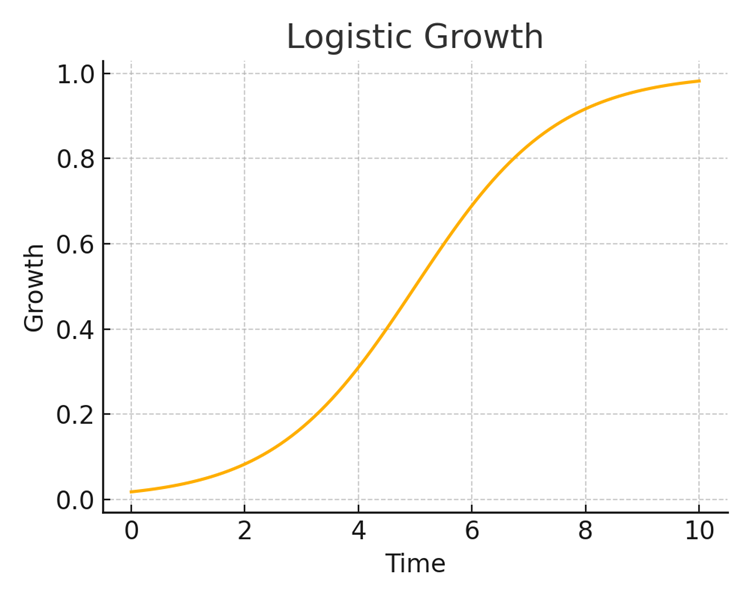
Also known as an s-curve, logistic growth is probably what most people think about with regards to learning. This is the “steep learning curve,” where skill gains accumulate rapidly early on and then start to slow. One example is fitness improvements—slow progress at the very beginning as we learn the basics, then rapid improvement, and then diminishing returns.

My sense is that most of the things we try to learn feel something like this—very difficult at first, when we are investing a lot of time and seeing little reward (this is when most of us give up), but then if we stick with it long enough, we start to see rapid gains in ability. Eventually, we get to a point where we have picked all of the low-hanging fruit and we hit a plateau, where additional time investment yields little result.

I don’t think plateaus are permanent, however. Every time I feel like I’ve hit a pleateau—whether in finance or in soft skills—after some time I discover an entirely new dimension of things that I don’t know, and I get to start a separate S-curve all over again from the bottom. I suspect the true experts in any field are those that have gone through 10, 20 s-curve phases of learning over the course of their careers.

The Emotional Dimension

I draw a few conclusions from these graphs.

First, starting early (or now) offers big benefits. Quadratic, exponential and logistic growth all require time in order to hit the sharp upward-sloping parts of their growth curves. Building an early foundation and then continually reinvesting yields large gains.

Second, in addition to time, we need patience. It’s easy to invest a small amount of time, not see any significant improvements, and then grow discouraged and quit. Continually reinvesting early on when the gains are small or not visible requires faith.

Finally, better-than-linear growth applies to things other than learning as well. For example, the value of networks grows quadratically and career advancement often follows s-curves. Focus and continued incremental investment of time can produce rewards on a scale that a linear-thinking mind has trouble estimating.

Next week, we’ll dive into how the human brain has a hard time understanding the impact of compounding and why people tend to use incorrect discount rates in order to make decisions in their personal lives.

Until then, our exercise!

Exercise

Journal on the following or discuss with a friend.

1)      Reflection

In what areas of my life have I already made significant investments of time—in developing a skill or other body of knowledge, in a particular career track, in building a network, or some other domain?

Which of these areas offer compounding benefits? Which are linear or unproductive?

2)      Evaluation

What did the growth curve of these time investments feel like? Were they linear, or did growth accelerate as I invested more time? Did growth level off after a while, like an s-curve?

How do I feel about my time investment? To what extent are emotions like gratitude or regret present? Where did I give up too early?

3)      Action

Understanding that growth is often not linear, how do I want to invest my time going forward?

Regarding my prior time investments, if I stopped, can I pick up where I left off? Do I still have accelerating growth in front of me once I shake the rust off?

Where do I want to continue investing, where I have already hit the point of exponential or quadratic returns?

What am I afraid to start, because the early part of the s-curve feels tedious and overwhelming? How will I feel when I hit the middle part of the s-curve, and things really start to take off for me?