This is Part 3 of my nine-part series connecting financial frameworks with personal growth.

1.      Finance as a Framework

2.      Assets = Liabilities + Equity: What You Own Comes with Strings Attached

3.      Assets = Liabilities + Equity 2: What You Have vs. What You Can Use

4.      Time Value of Money 1: The Power of Compound Interest

5.      Time Value of Money 2: Why Humans Use Bad Discount Rates

6.      Risk and Return 1: No Risk, No Return

7.      Risk and Return 2: Why Humans Are Bad at Calculated Risks

8.      Risk and Return 3: Diversification and Building Multiple Pillars of Resilience

9.      Conclusion: The Emotional Balance Sheet

 

Last week we talked about the time value of money, and how compound interest applies to areas of our lives other than money. This week, I want to take a different spin on the time value of money formula and discuss why human beings have such a hard time making short-term sacrifices for long-term benefits.

TVM: The Big Picture

The time value of money formula gives us a way to compare money now with money in the future. Last week, we focused on the importance of time, and making consistent investments that compound over a long period. This week, we are discussing the impact of the interest rate, or “r,” on ultimate returns, and why choosing the wrong “r” leads to bad decisions.

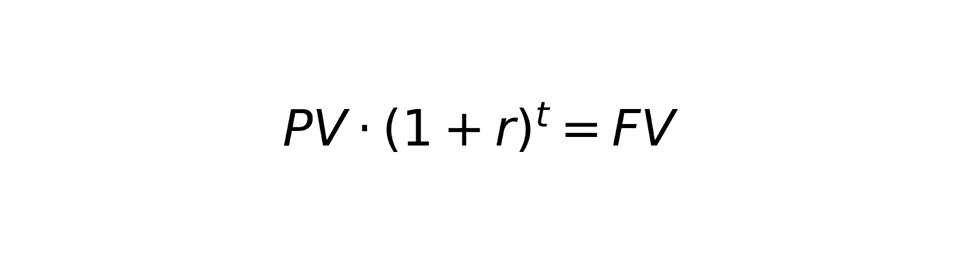
Last week, we discussed the basic compound interest formula above. This formula shows that an amount invested today (the present value) is multiplied by 1+an interest rate, which in turn is raised to the power of t, or the number of years it’s invested. That results in the future value. For example, $1000 invested at 5% for 3 years results in 1000*(1+.05)^3 = $1,157.625 at the end of 3 years.

This formula can be rearranged by dividing both sides by (1+r)^t as follows:

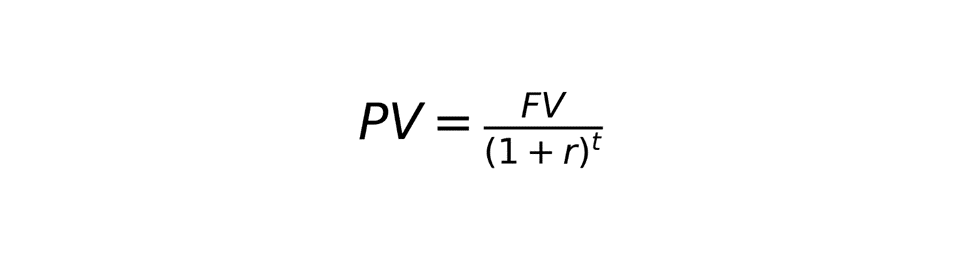
In this case, the formula shows the amount that needs to be invested (the present value) in order to have a given future value, if it’s invested at r rate for t years. This is known as the “discounting formula.” For example, if we know that we want to have $3,000 at the end of 3 years, and we can invest at 5%, the math would be

$3,000/(1+.05)^3 = $2,591.51

Meaning we need to invest $2,591.51 today, at 5% for 3 years, in order to have $3,000 at the end of 3 years.

Implications of the Discounting Formula

The relationship between PV and FV is governed by two variables—the interest or discount rate (“r”) and the number of years (“t”). Last week, we discussed how “t” has a very big impact on ultimate returns. This week, we are focusing on “r”.

For any given future value (let’s say $3,000), if r is high, the present value becomes less. For example, if we want $3,000 in 3 years, but we are able to invest at 10% instead of 5%, the math becomes

$3,000/(1+.10)^3 = $2,253.94

Said another way, not only do the years of compounding matter, but the discount rate (also known as the rate of return) also has a large impact on the amount needed to invest, or on the future amount.

Where Human Beings Get It Wrong

In addition to not intuitively understanding the impact of compounding over time, human beings are also bad at picking the right discount rates.

People basically don’t value benefits that come far into the future. Witness how many people feel regret, in old age, about not putting more attention into physical fitness or relationships with their children. Having these results requires making continual small investments over a period of many years, that, on a daily basis, people just refuse to make (most people will say, I’ll go to the gym tomorrow). Implicitly, what humans are doing is using a too-low discount rate to value the future benefit of health or relationships.

To demonstrate what I mean, let’s say that being fit at age 65 is worth 10,000,000 units of happiness more than having heart disease. Each day, a person has a choice of sitting on the couch (+10 happiness) or doing exercise (-10 happiness). Making the investment—bearing the cost—of doing the exercise requires us to assign a high rate of return to the investment. But most of us don’t do the exercise, which implies that we assign a low rate of return to putting in the effort now. Implicitly, the human mind feels that expending effort won’t yield much.

These numbers are arbitrary, but let’s walk through the math anyway. Assuming annual compounding (to simplify) and starting at age 25 (40 years), investing -3650 happiness per year, and reaching a +10,000,000 happiness at the end of 40 years, means that the return on investment was 16.53% annually. That sounds pretty good!

However, since most people don’t do this, it means they are assigning a low rate of return to the time investment now. For example, if people think that exercise yields returns of 5% annually on happiness, investing -3650 happiness per year for 40 years only yields future happiness at age 65 of +440,919, or more than 20x lower.

You might say that “well, people are using the correct discount rates, they just don’t value future benefits much.” The key here is that many people at age 65 feel the emotion of regret, which is an indicator that they made the wrong choice and wish they had done something different. The negative happiness of having heart disease is far greater than they realized.

Why Do Humans Use Low “r”s?

I think this comes down to evolutionary programming.

The human mind evolved 120,000 years ago, when lifespans were short and the environment presented physical danger at every turn. The mind was shaped to prioritize immediate benefits over long-term benefits because there might not be a long-term—eat the sweet fruit now (because calories might be scarce tomorrow), rest now (because we might get chased by a tiger in three hours), etc.

While society has become much safer and easier, that survival instinct—looking for short-term gains—hasn’t gone away. That’s why we reach for the chocolate chip cookie (instant calories now) and veg out on YouTube on the couch (preserve energy wherever possible).

Conclusion

Intellectually, we understand long-term benefits—a fit body, a stacked savings account, whatever. Emotionally, we don’t, because benefits now always feel more valuable than benefits later. Focusing on the long-term requires us to forcibly override this portion of evolutionary programming—in other words, assigning higher rates of return to present-day investments.

Over the next two weeks, we will return to the idea of evolutionary programming when we dive into risk, return, and how the human mind conceptualizes these things.

Exercise

Journal on the following or discuss with a friend.

1)      Review

Where in my life am I avoiding the short-term investments that are needed to achieve the long-term benefits that I say that I want?

These long-term benefits could be in actual finance (saving and investing), health, relationships, learning, hobbies, or some other domain.

2)      Noticing

At the exact moment when I decide not to make a short-term investment (e.g. standing up and going to the gym), what emotion do I feel?

What does that emotion imply about the rate of return my mind is implicitly assigning to the short-term investment?

3)      Action

Choose one area of your life where you want to commit to achieving a long-term benefit.

Can I assign a higher rate of return to my long-term goal? Can I make a short-term investment, telling myself that I am getting a higher return than what it feels like?

How does my willingness to take action change when I do this?